本文實例為大家分享了java實現(xiàn)Dijkstra算法的具體代碼，供大家參考，具體內(nèi)容如下

1 問題描述

何為Dijkstra算法？

Dijkstra算法功能：給出加權(quán)連通圖中一個頂點，稱之為起點，找出起點到其它所有頂點之間的最短距離。

Dijkstra算法思想：采用貪心法思想，進(jìn)行n-1次查找（PS:n為加權(quán)連通圖的頂點總個數(shù)，除去起點，則剩下n-1個頂點），第一次進(jìn)行查找，找出距離起點最近的一個頂點，標(biāo)記為已遍歷；下一次進(jìn)行查找時，從未被遍歷中的頂點尋找距離起點最近的一個頂點， 標(biāo)記為已遍歷；直到n-1次查找完畢，結(jié)束查找，返回最終結(jié)果。

2 解決方案

2.1 使用Dijkstra算法得到最短距離示例

此處借用文末參考資料1博客中一個插圖（PS：個人感覺此圖描述簡單易懂）：

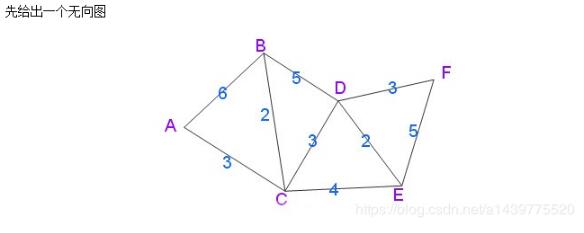
2.2 具體編碼

Dijkstra復(fù)雜度是O(N^2)，如果用binary heap優(yōu)化可以達(dá)到O((E+N)logN)，用fibonacci heap可以優(yōu)化到O(NlogN+E) 。

注意，Dijkstra算法只能應(yīng)用于不含負(fù)權(quán)值的圖。因為在大多數(shù)應(yīng)用中這個條件都滿足，所以這種局限性并沒有影響Dijkstra算法的廣泛應(yīng)用。

其次，大家要注意把Dijkstra算法與尋找最小生成樹的Prim算法區(qū)分開來。兩者都是運(yùn)行貪心法思想，但是Dijkstra算法是比較路徑的長度，所以必須把起點到相應(yīng)頂點之間的邊的權(quán)重相加，而Prim算法則是直接比較相應(yīng)邊給定的權(quán)重。

下面的代碼時間復(fù)雜度為O(N^2)，代碼中所用圖為2.1使用Dijkstra算法得到最短距離示例中所給的圖。

package com.liuzhen.chapter9;public class Dijkstra { /* * 參數(shù)adjMatrix:為圖的權(quán)重矩陣，權(quán)值為-1的兩個頂點表示不能直接相連 * 函數(shù)功能：返回頂點0到其它所有頂點的最短距離，其中頂點0到頂點0的最短距離為0 */ public int[] getShortestPaths(int[][] adjMatrix) { int[] result = new int[adjMatrix.length]; //用于存放頂點0到其它頂點的最短距離 boolean[] used = new boolean[adjMatrix.length]; //用于判斷頂點是否被遍歷 used[0] = true; //表示頂點0已被遍歷 for(int i = 1;i < adjMatrix.length;i++) { result[i] = adjMatrix[0][i]; used[i] = false; } for(int i = 1;i < adjMatrix.length;i++) { int min = Integer.MAX_VALUE; //用于暫時存放頂點0到i的最短距離，初始化為Integer型最大值 int k = 0; for(int j = 1;j < adjMatrix.length;j++) { //找到頂點0到其它頂點中距離最小的一個頂點if(!used[j] && result[j] != -1 && min > result[j]) { min = result[j]; k = j;} } used[k] = true; //將距離最小的頂點，記為已遍歷 for(int j = 1;j < adjMatrix.length;j++) { //然后，將頂點0到其它頂點的距離與加入中間頂點k之后的距離進(jìn)行比較，更新最短距離if(!used[j]) { //當(dāng)頂點j未被遍歷時 //首先，頂點k到頂點j要能通行；這時，當(dāng)頂點0到頂點j的距離大于頂點0到k再到j(luò)的距離或者頂點0無法直接到達(dá)頂點j時，更新頂點0到頂點j的最短距離 if(adjMatrix[k][j] != -1 && (result[j] > min + adjMatrix[k][j] || result[j] == -1)) result[j] = min + adjMatrix[k][j];} } } return result; } public static void main(String[] args) { Dijkstra test = new Dijkstra(); int[][] adjMatrix = {{0,6,3,-1,-1,-1},{6,0,2,5,-1,-1},{3,2,0,3,4,-1},{-1,5,3,0,2,3},{-1,-1,4,2,0,5},{-1,-1,-1,3,5,0}}; int[] result = test.getShortestPaths(adjMatrix); System.out.println('頂點0到圖中所有頂點之間的最短距離為：'); for(int i = 0;i < result.length;i++) System.out.print(result[i]+' '); }}

運(yùn)行結(jié)果：

頂點0到圖中所有頂點之間的最短距離為：0 5 3 6 7 9

以上就是本文的全部內(nèi)容，希望對大家的學(xué)習(xí)有所幫助，也希望大家多多支持好吧啦網(wǎng)。